All published articles of this journal are available on ScienceDirect.
Deterministic Chaos and Fractal Complexity in the Dynamics of Cardiovascular Behavior: Perspectives on a New Frontier
Abstract
Physiological systems such as the cardiovascular system are capable of five kinds of behavior: equilibrium, periodicity, quasi-periodicity, deterministic chaos and random behavior. Systems adopt one or more these behaviors depending on the function they have evolved to perform. The emerging mathematical concepts of fractal mathematics and chaos theory are extending our ability to study physiological behavior. Fractal geometry is observed in the physical structure of pathways, networks and macroscopic structures such the vasculature and the His-Purkinje network of the heart. Fractal structure is also observed in processes in time, such as heart rate variability. Chaos theory describes the underlying dynamics of the system, and chaotic behavior is also observed at many levels, from effector molecules in the cell to heart function and blood pressure. This review discusses the role of fractal structure and chaos in the cardiovascular system at the level of the heart and blood vessels, and at the cellular level. Key functional consequences of these phenomena are highlighted, and a perspective provided on the possible evolutionary origins of chaotic behavior and fractal structure. The discussion is non-mathematical with an emphasis on the key underlying concepts.
INTRODUCTION
Investigations into the behavior of physiological systems have traditionally placed great emphasis on the concept of homeostatic equilibrium, and how disturbances in homeostatic control can produce disease. The underlying assumption of this concept is that physiological systems exist at a steady state which can be switched to other states by a particular stimulus. However, biological systems are capable of more complex behaviors; there are patterns, rhythms and tempos to almost all biological processes from the level of the cell to that of the whole body. It is therefore important to take a step back and ask what the behavior of the system really is. Five kinds of physiological behavior are possible, and systems have the ability to move between them. Each has a precise mathematical definition, but can be understood intuitively as follows:
- Equilibrium describes a system at steady state, the classic view of physiological systems.
- Periodicity describes a system with a simple rhythm in which a cycle is repeated at a set frequency. This is seen in many circadian rhythms, such as the central and peripheral body clocks which control many of the other circadian rhythms in the body.
- Quasi-periodicity describes a more complex behavior produced because the system cycles with at least twofrequencies whose ratio is not a rational number. This is a common behavior in physiological systems; it is seen in the electrophysiological behavior of the heart and the nervous system.
- Deterministic chaos describes a system which is no longer confined to repeating a particular rhythm, and is free to respond and adapt. As is explained in more detail below, the system is constrained only by ‘boundary conditions’ imposed to prevent it from collapsing. Chaos is seen in a wide range of physiological systems, including the cardiovascular system.
- Random behavior represents a breakdown of order in the system. Its behavior is now uncoordinated.
The control of homeostatic equilibrium is the easiest behavior to study using our existing technological and mathematical tools, and this is why it was the first behavior to be systematically investigated by the scientific method. The study of circadian rhythms and temperospatial organization has led us into the periodic and quasi-periodic behaviors. Now the ability to study chaotic behavior is within reach, and we are standing on the edge of a new frontier in which we can begin to ask unbiased questions about the behavior of a system. Why is this important? The first reason is that the type of behavior determines the approach which can be used to study it. As discussed below, equilibrium, periodicity and quasi-periodicity can be studied using the reductionist approach, whereas deterministic chaos cannot.
The second reason is that it allows us to ask deeper questions about biology. What advantages do the different behaviors confer, how are they created and what are the consequences of moving from one kind of behavior to another? The aim of this review is to discuss how the emerging mathematical concepts of chaos theory and fractal mathematics are allowing us to approach these questions. The discussion will be non-mathematical, with an emphasis on the concepts, and will focus on the cardiovascular system. The cardiovascular system is a rich area for the study of dynamics, and it is a system in which clinical applications for chaos theory have already been found.
THE APPLICATION OF DYNAMICS TO THE STUDY OF PHYSIOLOGICAL BEHAVIOR
Dynamics is the branch of physics concerning the study of how motion is produced by the action of forces. When applied to biology, it is used to study how the behavior of a system is created and controlled. A system is considered dynamic if it is deterministic and obeys the causality principle. Determinism is a philosophical proposition, which states that every event is determined by an unbroken chain of prior occurrences. The causality principle, derived from Descartes’ Third Meditation, states that every effect has an antecedent and proximate cause. Random behavior is not a dynamic because it does not meet these two stipulations. A dynamic system can be linear or non-linear. In a linear system, the behavior of the entire system can be deduced by adding the behaviors of each of its components together. Small causes produce small effects and large causes, large effects. Equilibrium, periodicity and quasi-periodicity are examples of linear dynamics. The conventional reductionist approach excels in the study of linear systems, because it is possible to derive a complete description of the system by breaking it down into its component parts.
In a non-linear system, the parts of the system are not simply added together, but participate in a cascade of amplification. Because a non-linear system is more than the sum of its parts, a complete explanation of its behavior cannot be obtained by the reductionist approach. In the physical world, non-linear dynamics usually relate to discontinuous ‘sudden’ phenomena such as tornadoes, explosions or breakages. The non-linear dynamic most frequently encountered in biology is deterministic chaos. In a chaotic system, small changes in the initial conditions are amplified and have profound effects on the final state so that the behavior of such a system cannot be predicted over the long term. It is perhaps unfortunate that the term ‘chaos’ is used to describe this because mathematical chaos does not refer to complete disorder. It refers to an orderly system whose behavior is so complex that it appears to be random; the human mind cannot see the patterns in the raw data because it lacks the computational power to do so. However, the beauty of mathematics is that it gives us the power to transcend the limits of our intuitive understanding. The mathematics of chaos theory applies transformations to the raw data which ‘force’ the underlying patterns to be revealed. To understand how this is done, and what deterministic chaos is, it is worth considering the history of how chaotic behavior was first discovered.
Mathematical chaos was observed independently by a number of scientists and mathematicians in different fields before taking shape as a theory in the second half of the 20th century [1]. It was officially (and accidentally) discovered by Edward Lorenz in 1963 [2]. Lorenz was a meteorologist who was running a series of weather simulations, and wanted to see a particular simulation again. To save time, he entered data from a previous computer readout and started the simulation from its halfway point, expecting that this would make no difference to the final results. To his surprise, he found that the results of the new simulation were markedly different from the previous one, and traced the fault to the computer printout. The printout had approximated the 6 figure readout of the computer to 3 figures. This small difference in initial conditions (using a 3 rather than a 6 digit input) was enough to substantially alter the outcome of the simulation. Indeed, it is now known that, in non-linear systems, these differences are amplified by iteration in an exponential manner. This is the ‘butterfly effect’: a creature as meek as a butterfly can trigger a storm thousands of miles away simply by beating its wings. It does so because the tiny initial displacement of the air is amplified in a cascade. This phenomenon is called the ‘sensitivity to initial conditions’. Lorenz concluded that, because of this phenomenon, the behavior of a chaotic system such as the weather can never be accurately predicted in the long term.
In 1901, Willard Gibbs pioneered the use of phase space to represent the state of a system. However, it was the Belgian physicist Ruelle who first used this approach to study the behavior of chaotic systems, and this resulted in the discovery of the attractors of a chaotic system [3]. Phase space is an abstract two or three-dimensional space in which the x, y and z- axes are used to represent key parameters which describe the state of the system. The state of the system at any given moment can then be represented as a point in phase space; the process by which data are mathematically converted into a point in phase space is called embedding. The state of a dynamic system is continuously changing, and by plotting the different states of the system which arise over time on a phase space diagram, one obtains a graphical representation of all possible states of the system, and the behavior of the system is revealed (Fig. 1).
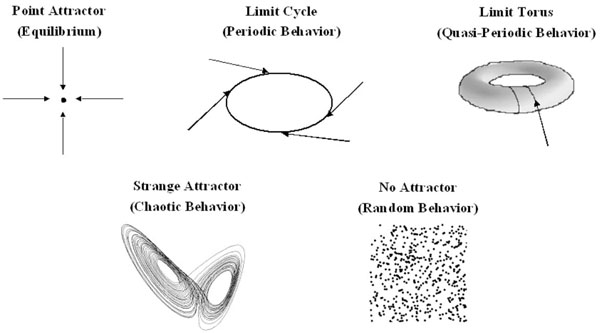
Possible states of a system represented in phase space. Equilibrium is represented as a point and periodic behavior as a cycle. Quasiperiodic behavior arises because the system is cycling with at least two frequencies whose ratio is not rational. A strange attractor is a sign of chaotic behavior, and has a low fractal dimension. The attractor shown is the Lorenz attractor. Random behavior produces a random scatter of points in phase space, with a high fractal dimension.
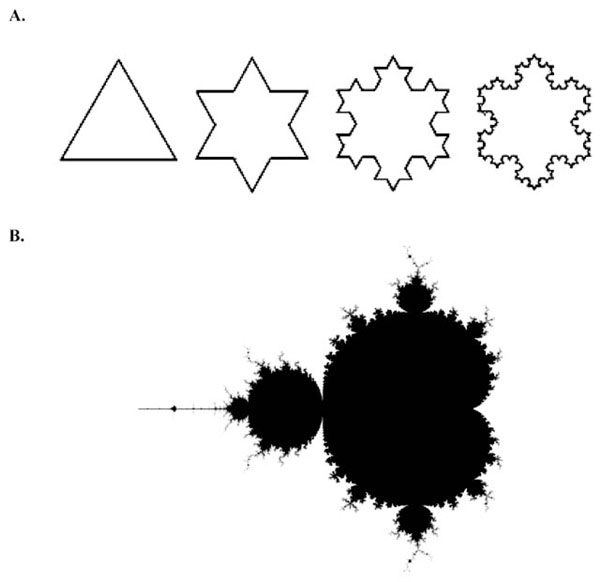
The first four iterations of the Koch Snowflake. (B). A visual representation of the Mandelbrot set, one of the best-known fractals.
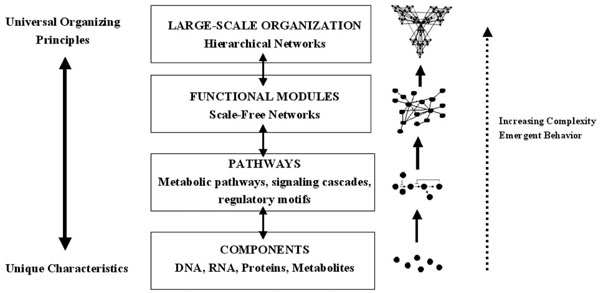
Increasing complexity in biological systems. Unique characteristics are conveyed by the individual components, which are then organized by universal principles. The components form pathways, then scale-free networks containing functional modules, then hierarchical networks. Emergent properties are seen with each increasing level of complexity (modified from [98]).
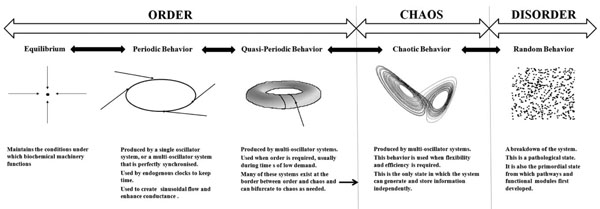
An overview of the relationship between dynamics and physiological function.
The motion of a dynamical system is driven by an underlying force, and most dynamical systems would come to rest in the absence of this force. Initial transient states of the system are therefore killed off with time and, under the influence of the driving force, the system evolves towards a particular state or behavior. If these events are followed in phase space, one sees that, given enough time, the state of a dynamical system evolves towards a particular set of points in phase space. This set is referred to as the attractor of the system, and this attractor is a property of a deterministic system [3]. A random system will never have an attractor. The attractor of a deterministic non-chaotic system can be a fixed point, a limit cycle (a periodic system) or a limit torus (a quasiperiodic system) (Fig. 1). In this case, the system is predictable, and will either loop continuously retracing the limit cycle or torus, or, in the case of a point attractor, settle at equilibrium. The attractor of a chaotic system is more complex and is referred to as a strange attractor. The points representing the state of the system loop endlessly within the boundaries set by the attractor, always towards a central point, but the trajectory traced by the point never repeats itself. The strange attractor contains an infinite number of possible trajectories through which the state of the system can cycle. Strange attractors are always fractals (discussed below), taking on beautiful shapes in phase space, which resemble such forms as butterfly wings, swirling clouds, spider’s webs or leaves.[1] Physiological systems can change their dynamics and move between periodicity, quasiperiodicity and chaos. In phase space, the attractor will change, ‘exploding’ into a chaotic attractor or ‘imploding’ into a limit torus or limit cycle. This phenomenon is termed ‘bifurcation’. If the system is moving toward chaos, the bifurcations are cascading it. If the system is moving toward quasiperiodic or periodic behavior, the bifurcations are creating negative feedback loops to stabilize it. This phenomenon gives the system a remarkable flexibility (see [1, 4-7] for a more complete discussion).
FRACTAL MATHEMATICS
This section provides a brief introduction to fractals and their properties. The reader is referred to a number of excellent books for a more complete discussion [4, 8-11]. Fractal mathematics is a fundamentally new kind of geometry, and one which remains unfamiliar to much of the scientific, medical and general communities. It has three applications in biology: the study of physical structure, the study of the structure of processes in time and the study of the dynamics underlying behavior (the attractor of a chaotic system is always a fractal). Our understanding of the form of natural objects has been dominated by the concepts of Euclidian geometry and calculus. However, Euclidian geometry is unable to describe many of the exquisite patterns with which nature is replete, such as the shape of a cloud, a tree or a snowflake. One of the reasons for this is that objects in the natural world have features which extend over many scales, and examination of an object at finer scales reveals new previously unseen detail. Euclidian geometry fails to describe this because it can only deal with one scale at a time; it describes figures whose edges are flat or curved and misses the detail.
In the 1970’s, Benoit Mandelbrot reported a new kind of mathematics, which he called ‘fractal mathematics’ [10]. The term fractal was derived from the latin word fractus, meaning broken, in order to reflect its defining features of self similarity and scaling. In the words of Mandelbrot, “ a fractal is a rough or fragmented geometric shape which can be split into parts, each of which is (at least approximately) a reduced-sized copy of the whole” [10]. Fractals can be observed throughout nature, from the small scale of atoms to the large scale of galaxies. The natural world is replete with examples: crystals, snowflakes, river networks, mountains, lightning, trees, webs, the list is long. The self-similarity of a fractal can be defined as perfect (geometrical) or statistical. Exact self-similarity represents the geometrically perfect fractal. A simple mathematical example of perfect self-similarity is given by the Koch snowflake (Fig. 2A). Starting with a straight line, a Koch snowflake is generated by substituting the middle third of the line with an equilateral triangle and repeating the process many times. The iteration vastly increases the length of the figure’s perimeter. After 40 iterations, a Koch snowflake generated from a 1-metre segment has a length which, if unwound, would stretch from the earth to the sun. Another example is the Mandelbrot set (Fig. 2B).
Nature never conforms to geometric ideals, and just as one would be hard-pressed to find a perfect sphere or cube in nature, one would be equally hard-pressed to find a fractal with perfect self-similarity. Most fractals in nature exhibit statistical self-similarity. Statistical self-similarity refers to a situation in which the fractal is approximately self-similar at different scales; the statistical properties of the part are proportional to the statistical properties of the whole. Examples of such self similarity in the human body include self-similar invaginations of alveolae and the intestinal tract which increase the surface area for absorption, or the self-similar branching pattern of the dendritic, bronchial and vascular trees [5, 12-15]. An important extension of the fractal concept is that fractals are not only observed in physical structures; biological processes in time also exhibit fractal properties in that fluctuations at a given timescale resemble the fluctuations of the same process observed at a smaller timescale. A classic example of this is seen in recordings of ion channel currents; self-similar patterns of ion channel opening are observed over several timescales [16]. The other extension is that the attractor of a chaotic system is always a fractal, and fractal geometry therefore has a role to play in describing dynamics.
For a fractal system, the measurement of any parameter depends on the resolution at which the measurement is taken. If one is measuring length, for example, the value of the measured length would increase as the finer details are revealed. There is therefore no one ‘true’ value of the measurement, but rather a relationship between the measurement and the resolution. This is referred to as a scaling relationship, and it poses two fundamental challenges to our existing analytical tools. The first is modest. If a fractal physiological system is studied at different resolutions, the measurements obtained would be expected to differ, and this may explain some of the measurement discrepancies found in the literature [17]. Biological fractals, however, are usually only self-similar over a few orders of magnitude, so this problem is overcome by studying the structure at the finest level of detail. The second challenge is profound, and it arises when studying fractal processes in time: fractals can have no mean and infinite variance! How is this possible?
We are used to using means and variances to describe datasets, and the sample mean we obtain by experiment is meant to reflect the population mean of the parameter. As the sample size is increased, the sample mean should approach the value of the population mean. This does not happen for fractals: as the sample size increases, the value of the sample mean continues to change and diverge to either zero or infinity, never approaching a ‘true mean’. This situation arises because the value of the parameter depends on the scale at which it is measured, and can therefore never have a single true value. Self-similarity at multiple scales can also affect variance, because smaller fluctuations in the data are amplified as the resolution is increased. The measured variance increases as the sample size or sample time increases, and tends towards infinity. This poses fundamental problems to the approach of statistical hypothesis testing (see [4] for review). Firstly, we always rely on the mean and variance of our measurements to define the parameters of the system being studied. However, if there is no mean and infinite variance, there is no way to determine what the parameters of the system are, so we have no way of detecting a change in those parameters. Furthermore, because there is no true mean of the system, the value of the calculated mean will be seen to change even if the underlying process remains unchanged. This means that, if we wish to look for changes in the state of a fractal system, we cannot use our existing analytical tools because they are essentially blind.
It is clear that we need new analytical tools to study fractals, but our ability to describe the properties of fractals is still rudimentary. The major parameter which has been described is the fractal dimension, a measure of a fractal’s space-filling properties. Put another way, fractal dimension measures the extent to which the irregularities of a fractal embedded on a curve spread out into the second dimension, or the extent to which the irregularities of a fractal embedded on a surface spread out into the third dimension. Fractals always have fractional dimensions (e.g. 1.7, 2.3 etc), which is a counter-intuitive idea when first encountered, but it can be understood by considering the familiar Euclidian shapes. Euclidian geometric shapes completely ‘break into’ the next dimension (e.g. line to square to cube) without creating detailed structure along their edges. The fraction (1.7, 2.3) represents the detail that Euclidian geometry misses; it describes the existence of a detailed structure along the edge of the shape. The dimension of the curve, surface or solid in which the fractal is embedded is referred to as the topological dimension, and is always an integer (1, 2 or 3). A fractal is defined mathematically as a set of numbers for which the fractal dimension is greater than the topological dimension [10].
THE APPLICATION OF FRACTAL MATHEMATICS TO CHAOS THEORY
As discussed above, the attractors of a chaotic system are always fractals. The fractal dimension of the attractor provides an indication of how deterministic the system is. If the fractal dimension is low, then the data would have been generated by a deterministic system. If the fractal dimension is high, then the data would have been generated by a random system. The reason for this can be understood intuitively as follows. As the fractal dimension increases, the form of the fractal is seen to disperse and increasingly resemble a random scatter of points. A random scatter of points in phase space is indicative of a truly random system.
CIRCADIAN RHYTHMS
Equilibrium needs little discussion here; it has been a core concept of biology for decades. We can begin our consideration of physiological behavior by briefly examining periodic behavior as exemplified by circadian rhythms. Circadian rhythms can be influenced by exogenous factors; indeed, exogenous factors (lifestyle, sleep patterns, stress) have a profound influence on the circadian rhythms of heart rate and blood pressure [18]. However, there is a component of the rhythms which is endogenous. These rhythms are cycles of behavior which are driven by an internal oscillator and repeat themselves on an hourly basis for ultradian rhythms or on a 24-hour basis for circadian rhythms [19]. The endogenous component of the circadian rhythms is regulated by a circadian pacemaker or ‘clock’ which is intrinsic to the cell and self-sustaining. The clock maintains its function in the absence of environmental stimuli, but has a ‘reset’ mechanism which is responsive to environmental signals. The molecular basis for circadian clocks is a group of transcriptional and translational feedback circuits which have evolved to have a periodicity of approximately 24 hours. There is a master circadian pacemaker in the suprachiasmatic nucleus (SCN) which regulates peripheral clocks located in a wide range of tissues [19, 20]. The SCN pacemaker receives information about the time of day from light signals delivered via the retinohypothalamic tract. The synchronization of the peripheral clocks is achieved by neurohormonal stimuli and, most importantly, metabolic cues [21, 22]. There are circadian patterns present in cardiovascular and hemodynamic parameters such as heart rate, blood pressure, endothelial function and fibrinolytic activity. These rhythms may have pathophysiological significance, because there are also diurnal variations in the incidence of acute cardiovascular events (myocardial ischemia and infarction, cardiac arrhythmias, sudden death in heart failure) [23, 24]. The precise nature of the links between the rhythms and adverse cardiovascular events is the focus of much research. The peripheral clocks have been found to regulate a wide range of genes, including genes involved in metabolism, vascular integrity and responses to injury and pathological stimuli [20]. The function of the clocks can also be disrupted in disease states; this can manifest as a dampening of the oscillations (e.g. pathological cardiac hypertrophy) or a phase shift (e.g. diabetic cardiomyopathy) [25, 26].
Significant technological and analytical advances are needed before the dynamics of circadian clocks can be studied in detail. However, it is clear from existing evidence what the dynamics of the system are likely to be. The healthy state of this multi-oscillator system appears to be one of orderly, periodic, synchronous oscillations. Since the periodicity of the clocks is essential to their function, any bifurcation away from this behavior would be self-defeating. The system needs to be far enough away from the border between order and chaos to prevent chaotic behavior, but also far enough from equilibrium to maintain periodic dynamics. This reliable order is bought at the price of a lack of flexibility. This disadvantage can be seen in the way the system responds to challenges. The central and peripheral clocks are slow to respond to permanent changes in the timing of the sleep-wake cycle (2 days for the central clock, 8 days for the peripheral clocks) [27]. This rigidity helps to prevent unnecessary adjustments of the clocks in response to, for example, an afternoon nap. However, in the presence of more permanent behavioral changes such as shift work, it may be an important cause of disease [20, 28].
BLOOD FLOW AND VASCULAR FUNCTION
Although mean blood pressure exhibits a simple diurnal variation which is essentially periodic, the cardiovascular system is capable of more complex behaviors. These are generated both in the blood vessels and in the heart. Part of the complexity arises from the basic structure of the cardiovascular system. The heart and the vasculature contain structures which have a fractal-like appearance. Examples of structural fractals include the venous and arterial vascular trees, the organization of muscle fibres (bundles, fibres, fibrils, myofilaments), the arrangement of the His-Purkinje network in the heart and the structure of cardiac connective tissues (e.g. the chordae tendinae and aortic valve leaflets) [4, 5, 29, 30]. Living organisms possess complex, spatially distributed systems which depend on a vascular supply for their survival. The function of fractal networks such as the vascular tree is to achieve fast and efficient transport across these systems, and there is good evidence that the use of a fractal branching system minimizes the work of transport [31-33]. Although the scale-range of self-similarity is infinite for geometric fractals, in biology there is only a finite range over which self-similarity is observed. For the vascular tree, there are at least three orders of magnitude which are self-similar, from the larger feeder vessels (c. 5mm for small mammals) to the smallest arterioles (c. 10-20μm for small mammals). The small capillary networks into which the arterioles feed have a different topology to the rest of the vascular tree and are not part of the fractal network.
The fractal structure of the vasculature has profound consequences for animals, and it is worth pausing to reflect on this. One such consequence is physiological time. The classical Newtonian view of time is chronological time, in which time is viewed as being universal and above nature. This perspective of time is imposed by evolution in the form of ultradian and circadian rhythms, and we regulate our daily lives by it. However, Meyen proposed an alternative view in which time is related to variability and change, so that each self-contained system has its own time defined by specific events that occur within that system. Psychological time is an example of Meyen’s concept in which perceptions of the flow of time are dependent on the situation; time flies when we are busy, and grinds to a halt when we are waiting. The concept of physiological time arises from Meyen’s perspective and is defined by Boxenbaum as “a species-dependent unit of chronological time required to complete a species-independent physiological event” [34].
In order to maintain body temperature in the face of an impaired ability to lose heat, all the physiological processes of a larger animal are slower than those of a smaller animal (heart rate, respiration rate, movement etc.); the heart rate of an elephant is 30 beats per minute whereas that of a shrew is 1000 beats per minute. However, a shrew and an elephant get through the same number of heartbeats and respirations over the course of their lives (approximately 200 million breaths and 800 million heartbeats), and therefore live an equivalent amount of physiological time [35]. In chronological time, the elephant takes longer to use up its allotted beats and breaths, and therefore lives longer by living slower. It is well known that the relationship between the pace of physiological processes and animal size obeys a power-law function, so does it have a fractal origin? Metabolic rate is limited by the rate at which nutrients and oxygen can be supplied to the metabolic tissues, and this supply is constrained as the transport distances covered by the transport network are increased. The transport network, as discussed above, is fractal over three orders of magnitude. In the model proposed by Brown, Enquist and West, the fractal nature of the transport networks explains the power law relationship between metabolic rate and animal size [36, 37]. The implication of this theory is that the fractal structure of the vasculature has, over the course of evolution, exerted an influence on species’ physiological time and ultimately on their lifespan. It is remarkable that a fractal, which can often be represented by very simple equations, can influence a species’ own experience of time and ultimately set constraints on how long it will live.
The basic pattern of blood distribution is fractal, and this is imposed both by the anatomy of the vascular tree and by the local regulation of vascular tone [38-46]. Superimposed upon this basic pattern is a complex rhythm of vascular flow. It is well-established that blood vessels exhibit rhythmic changes in diameter which beget rhythmic changes in resistance [47, 48]. This behavior has been found to bifurcate between quasi-periodicity and chaos. The origin of the chaotic behavior lies not in the heart rate or neuronal control of the blood vessels, but in chaotic dynamics of the vasomotor response [49-51]. The chaotic behavior is produced by the interaction of two calcium oscillators in the cytoplasm, one of which is a fast oscillator maintained by voltage-dependent calcium uptake, and the other of which is a slower oscillator maintained by calcium-induced calcium release [52]. Chaotic behavior is prevented by nitric oxide and various purines, and inhibition of either of these is associated with the induction of chaotic vasomotion [6, 53]. Chaotic behavior can be induced by physically decreasing the perfusion pressure. These data indicate that blood pressure can act as a toggle between order and chaos in the control of vasomotion [49]. Vasodilator substances which lower the local pressure by increasing vessel diameter maintain the system in periodic dynamics.
Vascular conductance is improved by periodic sine-wave vasomotion, so the appearance of chaotic behavior in the blood vessel is detrimental to blood flow [53, 54]. Chaotic behavior has been observed in systemic blood pressure, and has been suggested to be partly attributable to chaotic fluctuations in peripheral vascular resistance produced by chaotic vasomotion [55-57]. However, if blood pressure variability is examined in the whole animal, further information about the origin of chaotic behavior is revealed. Nitric oxide inhibitors decrease the chaotic behavior of blood pressure variability, which is consistent with their influence on chaotic vasomotion [58, 59]. Intriguingly, blockade or stimulation of adrenergic α-receptors has the same effect [58, 59]; the decrease in complexity produced by the agonist could be related to a decrease in sympathetic tone mediated by the baroreceptor reflex. Denervation of the baroreceptors also decreases chaotic behavior of blood pressure variability [60]. Blockade of β-adrenoceptors or of the parasympathetic nervous system with atropine has little or no effect on overall complexity [58, 59], suggesting that chaotic behavior is regulated by the sympathetic nervous system at the level of the resistance vessels. Overall, these results suggest that chaotic behavior of the blood pressure is likely to reflect the regulation of tone in the resistance vessels; periodic vasomotion is induced by any factor which decreases the local pressure, and the influence of the sympathetic nervous system on blood pressure variability may reflect a local influence on vasomotion mediated by changes in local pressure. However, blood pressure is regulated by a wide range of factors and it is likely that there are other contributors to the chaotic behavior evident in blood pressure variability.
FRACTAL COMPLEXITY AND CHAOTIC BEHAVIOR IN THE HEART
It is well established that beat-to-beat variability exists in the heart rate; ‘regular sinus rhythm’ is, in fact, anything but. This variability was classically regarded as random, but is now known to exhibit fractal properties in time, and to exhibit chaotic behavior, indicating that the variability is in fact deterministic. The analytical methods employed to study this determinism have been reviewed recently [9], so this discussion will focus primarily on the concepts. It is presently unclear what the underlying mechanism is for cardiovascular chaos, although it appears to be related to the function of the autonomic nervous system. Heart rate variability and the sensitivity to initial conditions are attenuated when the parasympathetic nervous system is blocked by atropine, and enhanced by blockade of the sympathetic nervous system using the β-blockers propanolol or atenolol [58, 59, 61, 62]. Chaotic behavior is not influenced by classic pharmacological modulators of the blood vessels such as nitric oxide synthase inhibitors or agonists and antagonists of α-adrenergic receptors, suggesting that it is the direct action of the autonomic nervous system on the heart which is important [58, 59, 61, 62]. It is clear that chaotic behavior is increased when parasympathetic activity exceeds sympathetic activity; this effect is demonstrable when the sympathetic and parasympathetic nervous systems are inhibited. However, the reflex cardiac parasympathetic cardiac activity induced by nitric oxide synthase inhibitors does not produce an increase in cardiac chaotic behavior. This may simply reflect the fact that the parasympathetic nervous system is already exerting its maximum effect on the heart rate dynamics; removal of sympathetic drive may further increase chaos in part because it is a physiological antagonist of the parasympathetic drive, acting at a distinct site. Differences in the degree of chaos seen in the heart are likely to reflect differences in the ‘drive’ which maintains the dynamics of the system; the bifurcation of the system from order to chaos should be a threshold effect.
The dynamics of the heart rate can also be examined using fractal analysis, and heart rate variability has been found to exhibit self-similarity [63, 64]. The importance of the fractal structure is that the self-similarity extends over many timescales; this confers the effect of memory on the system. The heart is able to repeat beating patterns it has previously used. However it is not ‘remembering’ the rhythms per se; by assuming a fractal structure in time, the system is using a basic law of mathematics to achieve the effect of memory. Fractal structure appears to be related, at least in part, to the presence of chaotic behavior and can be lost by bifurcations towards either order or randomness.
If one studies the effects of pharmacological interventions on fractal complexity of the time series, the patterns are not the same as those seen for chaotic behavior. Denervation of the heart increases the fractal complexity of the heart rate, indicating that the fractal complexity has its origin in the heart itself, and is modulated by the autonomic nervous system [65]. Intriguingly, both the sympathetic and the parasympathetic nervous systems appear to decrease the fractal complexity of the heart rate variability [66-69]. Chaotic behavior and fractal complexity of the time-series therefore reflect different properties of the heart which respond differently to pharmacological interventions; atropine, for example, decreases chaotic behavior but increases fractal complexity. What are the differences between chaotic behavior and fractal complexity? Fractal analysis essentially reveals the structure of the signal, whereas chaos theory examines the underlying dynamics of the system that generates the signal. Fractal structure is therefore a more superficial measure of the state of the system, but it is easier to apply and has found clinical applications.
Fractal complexity and chaos are related to pathology in two clinical scenarios. In the setting of acute cardiovascular events such as myocardial infarction or arrhythmias, increased fractal complexity is associated with increased mortality, and is a superior predictor of mortality compared with more conventional measures of heart rate variability [65, 70-76]. The reason for this correlation is unknown. If one considers the dynamics of the heart in this setting, arrhythmias appear to represent a state in which the system is driven away from the border between order and chaos and towards true randomness; in this context, the increased chaos may be regarded as harmful. There has been much discussion over whether increases or decreases in chaotic behavior are beneficial or harmful in the context of acute cardiac events. There are two aspects of chaos to consider. The first is where the chaos occurs. Helpful chaotic behavior is probably due to chaotic behavior in the sinoatrial node.[77] However, if chaotic behavior appears independently in the rest of the conduction system, this may interfere with the cardiac cycle and be harmful. The second is whether the system is being maintained close to the border between order and chaos; any movement away from this border could be harmful, be it towards randomness or periodicity. There are therapeutic implications for this. It has been found that, with the use of properly timed stimulation delivered through pacemakers, the heart can be stimulated to bifurcate from chaos to periodic behavior (chaos control) or from periodic behavior to chaos (chaos anti-control). This approach has been used as a novel approach to treat arrhythmias, and both chaos control and chaos anti-control have been advocated as strategies [78-80].
By contrast, in the setting of chronic heart failure, fractal complexity is decreased, and in this case it is the decrease in complexity which is associated with increased mortality [81-84]. When fractal complexity breaks down, the breakdown can reflect a cascading of the system into true randomness or a reversion into periodic order. Heart failure may cascade the system in either direction, producing random or periodic behavior; in both cases the fractal complexity is seen to decrease, and in both cases the effect is associated with increased mortality [85]. Fractal complexity and chaotic behavior of the heart have both been found to decrease with ageing, and this loss of complexity is also believed to be detrimental (see [7, 86] for recent reviews).
Why is the loss of chaotic behavior harmful? Loss of chaotic behavior clearly creates a loss of flexibility in the system. However, it also leads to a loss of information storage and generation [5, 87, 88]. The ability to store and transmit information is lost because random behavior is meaningless, and periodic behavior simply repeats the same information over and over again. This is reflected in the loss of fractal complexity in the heart rate signal; the ‘memory effect’ conferred by the fractal structure is lost. Chaotic behavior is unpredictable behavior, and unpredictable behavior allows for a physiological ‘freedom of expression’; the key to generating useful information is the ability to change. In a recent review, Goldberger [89] pointed out that many disease states could be regarded as producing a breakdown in complexity, leading to ordered periodic behaviors:
“To a large extent, it is these periodicities and highly-structured patterns – the breakdown of multi-scale complexity under pathological conditions – that allow clinicians to identify and classify many pathologic features of their patients.” [89].
Where does chaotic behavior in the heart come from? Chicken embryo heart cells provide one of the best examples of physiological chaos ever observed [90, 91]. Pacing is a basic property of cardiomyocytes, and chicken embryonic heart cells are seen to spontaneously beat in a regular fashion. When an external electrical stimulus is applied, the timing of the next endogenous beat is altered; it can occur sooner or later. The system is therefore driven by two bio-oscillators; the internal oscillator of the cell’s own pacing rhythm, and the external electrical impulses [90, 91]. The cells will beat with regular periodicity in response to some external rhythms, but will revert to their own endogenous rhythms in response to others. This is chaotic behavior, with bifurcations induced by the external applied rhythm. The effect is to introduce beat to beat variability. In the intact heart, the property of spontaneous self-excitation is a property of all the excitable tissue found therein, but the pacemaker of the heart is the sino-atrial node. The path of excitation from the sinoatrial node, through the atria to the atrioventricular node and then to the His-Purkinje network generates the classic familiar pattern of the electrocardiogram (ECG). Analysis of the ECG reveals that there are irregularities in the record, the same beat-to-beat variability observed when heart rate data are analyzed, and analysis of the ECG has revealed evidence of chaotic behavior [4, 92, 93]. In the normal setting, this chaos is good. Studies of the spatial evolution of the cardiac electrical activity have revealed that the electrical behavior of the heart can be understood, in part, in terms of reaction-diffusion processes. These processes produce spiral waves, a known precursor to chaotic behavior, which appear when the heart goes from normal rhythm to a tachycardia and then break up as the heart transitions to fibrillation and the system bifurcates towards harmful chaos [77]. This spatial evolution model suggests a mechanistic difference between the harmful chaos and the beneficial chaos. One could speculate that bifurcations in cardiac rhythm are harmful because these produce chaos in the conduction system. However, the chaotic variability of normal sinus rhythm is beneficial, because this represents an interplay between the conduction system and the heart muscle which confers efficiency and flexibility. How can chaotic behavior in the heart be permanently lost? An explanation is most likely to be found in the structural changes in the heart produced by pathology and by aging. The structural properties of the heart determine its ability to respond to stimulation; if the heart is less compliant due to remodeling, or there is a loss of cardiomyocytes, the mechanical function of the heart could be constrained and forced toward more periodic behavior. Chaos in the heart may not just arise in the conduction system. Metabolic pathways can bifurcate towards chaos, and metabolism is intricately related to function. Calcium handling is a key regulator of contractile force, and chaotic behavior within these pathways could beget chaotic behavior in the generation of contractile force.
Where does fractal complexity in the heart rate signal come from? To a certain extent, fractal complexity may reflect underlying chaos, and it is lost by a bifurcation away from chaos in either direction (towards order or randomness). However, some of the fractal complexity of the heart may have its own unique origins. If one considers the endogenous rhythms of the cardiomyocytes, a fractal structure may exist in the multioscillator system of the cardiac syncytium. If one considers the conduction system in the heart, there is a fractal structure to the His-Purkinje system, which could beget fractal organization of the heart rate signal. The relationship between fractal complexity and underlying chaos may not be as straightforward as the discussion in this review has so far assumed. This is clearly illustrated by the effects of the parasympathetic nervous system, which increases chaos in the heart rate, but decreases fractal complexity. The major influence of the parasympathetic nervous system is on the conduction system; the ventricles receive sparse parasympathetic innervation. It is possible that, by decreasing conduction through the heart, the parasympathetic nervous system releases some of the cardiomyocytes from the unifying influence of the His-Purkinje system and the dual oscillator system is more prone to chaotic behavior. At the same time, a decrease in the influence of the fractal His-Purkinje system produces a decrease in the fractal complexity of the signal. In this model, the conduction system is the origin of the fractal complexity, whereas the interplay between the conduction system and the heart muscle is the origin of the chaotic behavior. The sympathetic nervous system innervates the entire heart and increases the rate and force of contraction; it can impose order on the conduction system and the heart muscle, and may therefore drive the dual oscillator towards more periodic behavior. If the heart becomes more periodic in its behavior, fractal complexity of the heart rate will also decrease. This may explain why denervation of the heart increases fractal complexity; it would be the loss of the sympathetic drive which allows fractal complexity to increase.
CELLULAR DYNAMICS
The example of cardiovascular chaos illustrates that chaotic behavior at the level of the system is conferred by behavior at the cellular level. It is therefore important to consider the cellular level in more detail if the mechanistic bases of chaos and fractal complexity are to be understood. The central dogma of molecular biology implies the existence of a hierarchy within the cell in which each organizational level is given a particular task: DNA stores information, RNA processes information, proteins execute the programs and metabolites fuel and fine tune the programs. However, the true distribution of cellular functions within the cell is more complex than this. The proteome is the repository of short term information storage, the metabolome is an important controller of gene expression and RNA can execute cellular programs by influencing gene expression or regulating the subcellular targeting of the proteome [94-98]. It is therefore clear that, instead of being distinct levels in a linear chain, the genome, transcriptome, proteome and metabolome fulfil their functions by forming complex networks. Surprisingly, gene, protein and metabolic networks are all organized according to the same principles and form a type of network which is referred to as ‘scale-free’ [99]. In a scale free network, the number of interconnections formed by a node, referred to as its degree, obeys a power-law distribution i.e. there are groups of nodes which form large numbers of interactions, and others which form only a few; power law functions are characteristic of fractals, and the cellular networks can sometimes assume a fractal structure. Oltvai and Barabasi described this new paradigm in terms of a complexity pyramid in which the uniqueness conferred at the level of individual cellular components is integrated using common organizing principles [98]; this is summarized in Fig. (3).
Metabolic pathways represent an archetypal network in which to consider network dynamics. The topology of the metabolic network (substrate supply, energy production in the mitochondria, energy utilization) is scale-free. Within the network, evidence is emerging of compartmentalization. ATP generated by glycolysis is used to fuel membrane-bound transporters and ion channels in the sarcolemma and sarcoplasmic reticulum, whereas ATP generated by mitochondrial oxidative phosphorylation is targeted to cytoplasmic processes such as the generation of contractile force (see [100] for review). Chaotic behavior has been frequently related to the interaction that occurs between oscillators, and metabolic pathways are replete with them.
There are ultradian rhythms in oxygen consumption. Within the metabolic machinery, there are more irregular oscillators. A well-studied example is the matrix membrane potential, whose energy is harnessed to generate ATP. The matrix membrane potential undergoes asynchronous oscillations which are triggered by reactive oxygen species (ROS) in a feed-forward cycle of ROS-induced ROS release. The function of these oscillations is unclear, but they may represent a mechanism for clearing ROS. Weiss et al. proposed that if these fluctuations are asynchronous, the induction of oscillations could be used to ‘neutralize’ unneeded mitochondria at times of low energy demand. However, if the fluctuations become synchronous, all the mitochondria would synthesize and consume ATP according to a cyclic pattern in unison, and energy supply would be uncoupled from energy demand [100]. The switch towards synchronous fluctuations in membrane potential represents a loss of complexity in the system, a harmful bifurcation toward periodic behavior. Another well-studied metabolic pathway is glycolysis. Glycolytic flux can be constant or periodic when glucose is provided at a single constant level. When the input of glucose is periodic, glycolytic flux can be either periodic or chaotic depending on the amplitude and frequency of the glucose input [101, 102]. It is likely that most biochemical pathways can exist in a number of oscillatory states and can bifurcate from periodic to chaotic behavior. The study of such phenomena in biochemical pathways is limited by technology: it is not easy to track and record metabolites in real time as can be done with, for example, calcium.
The next level of organization to consider is communication between cells. Such communication can arise through the exchange or autocrine or paracrine factors, or occur through direct contact. Ultradian rhythms display fractal properties, and the oscillators present within cell populations have the intriguing ability to self-synchronize (see [103] for review). In the model of cell synchronization proposed by Brodsky, the coordinated signal to synchronize protein synthesis oscillations is a loss of gangliosides throughout the cell population. The resulting increase in intracellular calcium activates protein kinases which modulate the periods their target oscillators and produce a synchronous rhythm in the entire population [103]. However, the fractal structure of the multi-oscillator system is preserved. Cell-cell communication is of importance when considering phenomena such as the conducted vasomotor response which, as discussed above, can exhibit both periodic and chaotic behavior.
THE EVOLUTIONARY ORIGINS OF CELLULAR DYNAMICS
The evolutionary origins of the cellular dynamics described above can be understood using the concept of self organization. Self organization is a phenomenon first described by Alan Turing, in which repeated cycles of repulsion and attraction between units increase the internal complexity of a system, creating new levels of complexity without the direction of an external force or program [104]. Self-organization as a mechanism of evolution can be understood as follows. The initial behavior of the system is random; there are no meaningful interactions. However, because of their own properties, the components of the system will gradually start to interact with some of their neighbours and repel others. As the interactions become stronger, the system can bifurcate to become chaotic and then finally bifurcate again to become orderly. This process is exemplified by the spontaneity with which fish come together to form shoals or birds come together to form flocks. At the moment of self-organization, the dynamics of the system may bifurcate to create a new more complex behavior. In order for the new network to stabilize, the interactions of its components need to be strong so that repeated cycles of feedback can reinforce the new structure. However, if the interactions are too strong, the network will become rigid and lose its ability to adapt. When the principle of self-organization is applied to evolution, it is seen that self-organization can generate complex systems which are then moulded by natural selection until they exist at the boundary between order and chaos. The fully evolved system exists at the very edge of stability, and an intricate system of feedback, developed by evolution, keeps it there. When the system is pushed into chaotic behavior, the system quickly reverts back to order; this enables the system to maintain its flexibility without losing its structure [105, 106].
Little is known about how the first cellular networks evolved, but the principle of self-organization suggests a possible mechanism. Network dynamics in biological systems can be understood, at least in part, in terms of wave propagation through an excitable medium. It has been known for more than half a century that chemical reactions can spread in an oscillating manner akin to wave propagation. According to a theory first developed by Alan Turing, oscillations and chemical waves can self organize into a cellular network [104]. In this case, a chemical (e.g. a morphogen or second messenger) is synthesized rapidly at a particular location but diffuses slowly. At the moment of synthesis, a localized peak concentration is achieved. The chemical then diffuses into the surrounding medium and the concentration at the site of synthesis begins to fall. However, the next burst of synthesis gives rise to a second peak, and the process repeats itself.
Repeated intermittent ‘bursts’ of chemical synthesis result in a chemical oscillator which gives out chemical diffusion waves. Chemical oscillators can exhibit constant, periodic and chaotic behavior, behaving as a chaotic system with bifurcations [107]. The chemical diffuses out to interact with neighbouring processes and targets, and can elicit responses not only by its unique identity, but by its behavior in time. In addition, the site at which the chemical is synthesized enables site-specific responses to be elicited, which can lead to spatial organization of signaling, or contribute to the formation of architecture. As similar processes occur in parallel, the collective behavior of the system can suddenly bifurcate to produce a more complex behavior, and a functional module will have formed. Additional cytoplasmic structures can refine the function of the module. Aon et al. recently proposed a model based on the phenomenon of percolation, in which the cytoskeleton controls the paths that effector molecules take through the cell [108]; their model implies that the chemical diffusion waves can be directed and distributed, or blocked by the cytoskeleton. An example of the effects of cytoskeletal organization on a network is provided by the study of Aon and Cortassa, who found that increasing the extent of microtubular protein polymerization increased glycolytic flux in yeast [109].
Self-organization can create complexity independently, and provides an explanation of how function can gradually emerge from a sea of random behavior. However, if this is applied to evolution there is a major problem: how is the complexity passed on? Self-organisation, by definition, occurs without genetic influence, yet, in order for the complexity to survive in the species and be moulded by evolution, there must be traits to the new complexity which are heritable. It is unclear how complexity generated by self-organization can be propagated to an entire species, but knowledge of evolutionary processes permits some speculations. One would expect that the first time a new complex behavior appears, it will probably be lost. However, if a particular genetic background favors the generation of complex behaviors which improve survival, the favorable traits will be passed on and allow for the continued appearance of beneficial complex behaviors which will eventually survive in the species. The genome may gradually evolve to encode more of the behavior, essentially ‘recording’ it and leaving less to self-organization. The first step to testing this idea is to quantify genetic influences on traits believed to have arisen by self-organisation.
No studies have attempted to quantify genetic influences on chaotic dynamics as our technological and mathematical tools are not yet up to this challenge. However, structural traits can be more easily studied. Fractal structures are believed to form largely by self-organisation with limited genetic input. Recent studies have attempted to quantify genetic influence on fractal structure, but the data are conflicting. Glenny and coworkers recently quantified the genetic influence on flow distribution in the monozygotic offspring of armadillos, and concluded that 2/3 of fractal vascular geometry was determined by genetic influences [110]. The structure of the fractal retinal vasculature has been studied in monozygotic and dizygotic twins, and the genetic influence in this case was small – only vessel tortuosity was found to be genetically determined [111]. These initial studies do not allow any definitive conclusions to be drawn. However, there is probably a balance and a division of labor between the ability of a biological system to self-organize, and the imposition of instructions from the genome. This is an important and virtually untouched area of research.
THE INFLUENCE OF DYNAMICS ON FUNCTION
The choice of dynamics has important consequences for the function of physiological systems. The biochemical machinery of the cell has evolved to function under clearly defined conditions of pH, temperature, osmolarity, and at well defined levels of a host of electrolytes, nutrients and proteins. This is why the maintenance of equilibrium is important: the basic machinery which drives all functions is vulnerable to changes in these conditions. Periodic behavior is seen in the ultradian and circadian rhythms of the body. These evolved from the need to develop a sleep-wake cycle that is synchronised with the cycles of light and dark experienced on the earth’s surface. The clocks which drive circadian rhythms must maintain periodic behavior or they will lose their ability to keep time. Periodic behavior is also seen in the sine wave behavior of vasomotion; if this is lost, the movement of blood becomes less efficient. Quasiperiodic behavior is the most complicated behavior of linear dynamics and it defines the limits of order. It is seen in multi-oscillator systems such as the cardiac pacemaker. Many of these systems evolved to exist at the border between order and chaos and their function requires them to take advantage of both as the need arises. Chaotic behavior confers flexibility and efficiency on the system; it is usually beneficial, unless periodic behavior is integral to the function of the system as it is in the vasomotor response. Random behavior represents a complete breakdown of the system – fatal arrhythmias represent such a breakdown. Random behavior represents a complete breakdown of the system – fatal arrhythmias represent such a breakdown. Random behavior is also the initial behavior of unrelated components from which cellular networks first emerged. This paradigm is summarized in Fig. (4).
Fractal complexity in time is likely to be due, at least in part, to underlying chaotic behavior. Chaos gives the system the ability to generate and store information. Fractal complexity in time, such as that seen in the heart rhythm, is one example of this; it allows the system to repeat behaviors it has previously used. However, the system does not need to remember the behavior. Instead of developing a separate repository into which the information is saved, evolution has made the intriguing choice of using a basic law of mathematics to achieve the effect of memory. The loss of chaotic behavior in either direction (towards order or random behavior) leads to a loss of fractal complexity and a loss of this memory effect.
LIMITATIONS OF CHAOS THEORY AND FRACTAL MATHEMATICS
The use of fractal mathematics and chaos theory presents significant difficulties both at the level of the theory and at the level of application. At the present time, the properties of fractals are incompletely described, and further work is needed to discover new mathematical descriptors which can be applied to fractal analysis. However, the major drawback of fractal analysis is the lack of statistical tools which can determine whether differences in the properties of fractal objects or processes are significant. Because fractals have such bizarre statistical properties, this may require the development of a fundamentally new kind of statistics. Until these tools are developed, we are limited to asking if a structure or process has a fractal structure, and to what extent, which does not do justice to the true potential of the fractal concept. It also does not permit detailed mechanistic studies to determine the origin of fractal structure.
Chaos theory in its current form is also limited. At its present stage of development, it can be used to ask if experimental data were generated by a random or deterministic process, but it is a difficult and frustrating analytical approach to use. It is not clear how much data are required in order to construct the phase space set and determine its fractal dimension; the amounts of data are likely to be extremely large, and biological systems may not remain in a single state long enough to gather the required amounts of data. A low dimensional attractor is used as evidence of a deterministic system, but should be interpreted with caution; it is possible to produce a low dimensional attractor by constraining the choices available to a random process. A low dimensional attractor therefore does not definitively establish that a process is deterministic. There are also problems with artifacts introduced because of the sampling interval used to collect the data or inappropriate assumptions in the actual equations used to transform the raw data. Finally, there is also the problem of statistical hypothesis testing. Bifurcations are easy to detect and do not require statistical analysis. However, to detect more subtle changes in the attractor, a new statistical approach will be required.
CONCLUSION
To obtain an integrated understanding of physiology, we require an understanding of the complex dynamics of physiological systems. The full promise and potential of fractal mathematics and chaos theory remain to be realized, and await further development of the theories. Nevertheless, these concepts have already provided revolutionary insights into the nature of living things. A new frontier has been opened.
FURTHER READING
“Fractals and Chaos Simplified for the Life Sciences” [112] is a very accessible and visual text which provides a solid introduction to the mathematics and its applications to biology. “Fractal Physiology” [4] and “Fractal Geometry of Biological Systems” [8] provide more detailed reviews without assuming a strong mathematical background. “Fractals Everywhere” is a more thorough text for those who wish to study the mathematics in greater detail [11]. The groundbreaking work of Mandelbrot is worth reading, not least for the eloquence and beauty with which the concepts are presented and discussed [10].
ACKNOWLEDGMENTS
I would like to thank Dr. J.H. McNeill for helpful review of this manuscript, and Mr. P. Dhillon who first drew my attention to fractal mathematics.