In the Echo examination for patients with mitral regurgitation, the left ventricular pressure can be expressed as:

Where ΔP is the pressure gradient between left atrium and left ventricle; LDM is for left ventricular diastolic time constant in mitral regurgitation patients. Substituting Eq. (4) into Eq. (5LDM) and employing simplified Bernoulli’s equation:

ΔP=4v² leads to the following equation:

e^-t/T+B+ C = ΔP + LAP = 4v² + LAP

Or:

A natural logarithmic transformation on both sides of the above equation results in the expression:

Three points, (t1, 1m/s), (t2, 2m/s) and (t3, 3m/s), are then chosen on the descending limb of the mitral regurgitation continuous-wave Doppler velocity curve Fig. (1), which produces the following three equations:

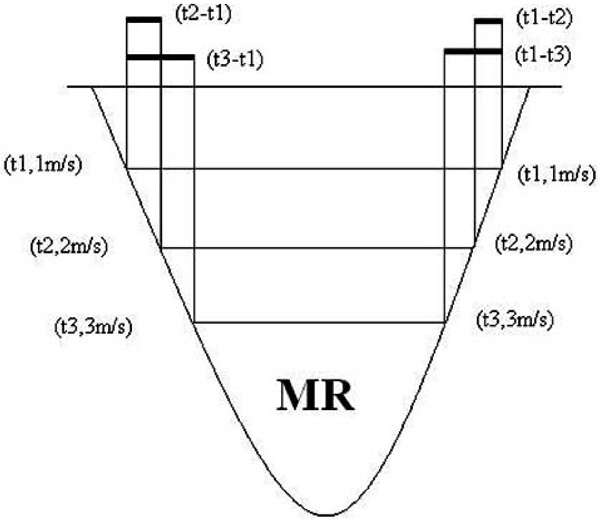
Fig. (1). A depiction of continuous wave Doppler mitral regurgitation spectrum where left ventricular diastolic time constant is calculated on the descending branch (right); left ventricular systolic time constant is calculated on the ascending branch (left).

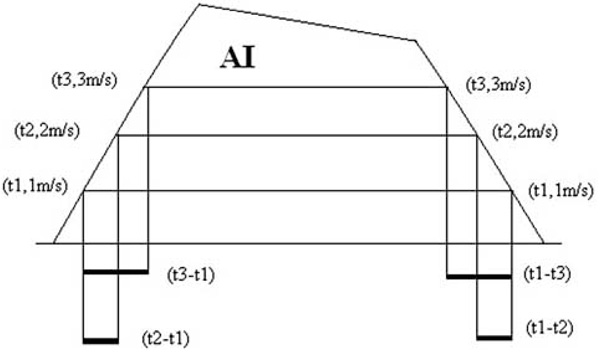
Fig. (2). A depiction of continuous wave Doppler aortic regurgitation (insufficiency) spectrum where left ventricular diastolic time constant is calculated on the ascending branch (left); left ventricular systolic time constant is calculated on the descending branch (right).

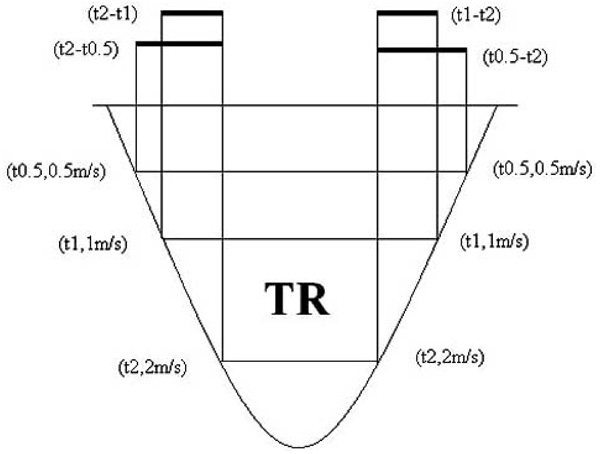
Fig. (3). A depiction of continuous wave Doppler tricuspid regurgitation spectrum where right ventricular diastolic time constant is calculated on the descending branch (right); right ventricular systolic time constant is calculated on the ascending branch (left).

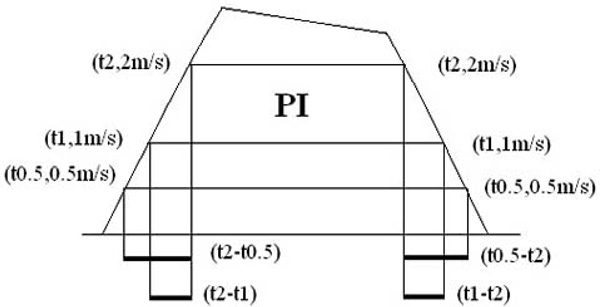
Fig. (4). A depiction of continuous wave Doppler pulmonary regurgitation (insufficiency) spectrum where right ventricular diastolic time constant is calculated on the ascending branch (left); right ventricular systolic time constant is calculated on the descending branch (right).

From the difference comparison of Eqs. (8LDM1) and (8LDM2), we find:

$\left(t1t2\right)T=\mathrm{1n}\left(41^2+\mathrm{LAP}C\right)\mathrm{1n}\left(42^2+\mathrm{LAP}C\right)$

Or:

Similarly,

From the above formulas (9LDM1) and (9LDM2), both Tau and (LAP-C) can be solved after we measure two time intervals: (t1-t3) and (t1-t2). Fig. (1) shows how measurement is done.

In the Echo examination for patients with aortic regurgitation, the left ventricular pressure can be expressed as:

Where ADP is the aortic diastolic pressure, ΔP is the pressure gradient between aorta and left ventricle; LDA is for left ventricular diastolic time constant in aortic regurgitation patients. Substituting Eq. (4) into Eq. (5LDA) and employing the simplified Bernoulli’s equation: ΔP=4×v² leads to the following equation:

$e^{tT+B}+C=\mathrm{ADP}P=\mathrm{ADP}4v^2$

Or:

A natural logarithmic transformation on both sides of the above equation results in the expression:

Three points, (t1, 1m/s), (t2, 2m/s) and (t3, 3m/s), are chosen on the ascending limb of the aortic regurgitation continuous-wave Doppler velocity curve Fig. (2), and substituted into Eq. (7LDA) respectively, which produces the following three equations:

From the difference comparison of Eqs. (8LDA1) and (8LDA2), we find:

$\left(t1t2\right)T=\mathrm{1n}\left(\mathrm{ADP}41^{2}C\right)\mathrm{l}n\left(\mathrm{ADP}42^{2}C\right)$

Or:

Similarly,

From the above formulas (9LDA1) and (9LDA2), both Tau and (ADP-C) can be solved after we measure two time intervals: (t3-t1) and (t2-t1). Fig. (2) shows how measurement is done.

In terms of location and time, cardiac function includes right ventricular diastolic function, right ventricular systolic function, left ventricular diastolic function and left ventricular systolic function. Each of the above mentioned “cardiac functions” begins with an isovolumic period when both the inflow and outflow valves close simultaneously. Apparently, this isovolumic period is a golden period to measure cardiac function since ventricular pressure change is not influenced by either preload or afterload.

Our hypothesis is that the time constant can be extended to all other “cardiac functions”. This means Eq. (4) is not limited to left ventricular diastole, but can also be applied in left ventricular systole, right ventricular diastole and right ventricular systole. Correspondingly, we will have the left ventricular systolic time constant, right ventricular diastolic time constant and right ventricular systolic time constant.

Such a hypothesis is based on the following premises: 1. Left ventricular diastolic time constant is suggested because left ventricular diastolic process is an active process. [1] Left ventricular systolic process is also an active process, so are right ventricular diastolic and systolic processes. 2. During isovolumic period, the ventricle is like a sealed box with both inflow and outflow valves shut off. With the active ventricular muscle movement, it is sensible to imagine the pressure built within it is described by an index equation. 3. In continuous wave Doppler regurgitation spectra, all of the paired ascending and descending branches are almost symmetric, showing they experience a similar process and can be characterized by a time constant which dictates how “fast” the pressure changes within the ventricle.

Attempts are being made to use a similar strategy to develop new formulas to calculate the time constants for the other “cardiac functions”.

• In mitral regurgitation patients
  Formulas for the calculation of left ventricular systolic time constant in mitral regurgitation patients are developed with a similar mathematical method, except:
  Three points, (t1, 1m/s), (t2, 2m/s) and (t3, 3m/s), are chosen on the ascending limb of the mitral regurgitation continuous-wave Doppler velocity curve Fig. (1). The final formulas are:
  
  
  (9LSM1)  $\mathrm{Tau}=\left(t2t1\right)\mathrm{1n}\left(\left(4+\mathrm{LAP}C\right)\left(16+\mathrm{LAP}C\right)\right)$
  
  
  
  (9LSM2)  $\mathrm{Tau}=\left(t3t1\right)\mathrm{1n}\left(\left(4+\mathrm{LAP}C\right)\left(36+\mathrm{LAP}C\right)\right)$
  
  where LSM is for left ventricular systolic time constant in mitral regurgitation patients.
• In aortic regurgitation patients
  Formulas for the calculation of left ventricular systolic time constant in aortic regurgitation patients are developed with a similar mathematical method, except:
  Three points, (t1, 1m/s), (t2, 2m/s) and (t3, 3m/s), are chosen on the descending limb of the aortic regurgitation continuous-wave Doppler velocity curve Fig. (2). The final formulas are:
  
  
  (9LSA1)  $\mathrm{Tau}=\left(t1t2\right)/\mathrm{1n}\left(\left(\mathrm{ADP}C16\right)/\left(\mathrm{ADP}C4\right)\right)$
  
  
  
  (9LSA2)  $\mathrm{Tau}=\left(t1t3\right)/\mathrm{1n}\left(\left(\mathrm{ADP}C36\right)/\left(\mathrm{ADP}C4\right)\right)$
  
  Where LSA is for left ventricular systolic time constant in aortic regurgitation patients.

• In tricuspid regurgitation patients
  Formulas for the calculation of right ventricular diastolic time constant in tricuspid regurgitation patients are developed with a similar mathematical method, except:
  Three points, (t0.5, 0.5m/s), (t1, 1m/s) and (t2, 2m/s), are chosen on the descending limb of the tricuspid regurgitation continuous-wave Doppler velocity curve Fig. (3). The final formulas are:
  
  
  (9RDT1)  $\mathrm{Tau}=\left(t0.5t2\right)/\mathrm{1n}\left(\left(16+\mathrm{RAP}C\right)/\left(1+\mathrm{RAP}C\right)\right)$
  
  
  
  (9RDT2)  $\mathrm{Tau}=\left(t1t2\right)/\mathrm{1n}\left(\left(16+\mathrm{RAP}C\right)/\left(4+\mathrm{RAP}C\right)\right)$
  
  Where RAP is for right atrial pressure and RDT is right ventricular diastolic time constant in tricuspid regurgitation patients.
• In pulmonary regurgitation patients
  Formulas for the calculation of right ventricular diastolic time constant in pulmonary regurgitation patients are developed with a similar mathematical method, except:
  Three points, (t0.5, 0.5m/s), (t1, 1m/s) and (t2, 2m/s), are chosen on the ascending limb of the pulmonary regurgitation continuous-wave Doppler velocity curve Fig. (4). The final formulas are:
  
  
  (9RDP)  $\mathrm{Tau}=\left(t2t1\right)/\mathrm{1n}\left(\left(\mathrm{PDP}C4\right)/\left(\mathrm{PDP}C16\right)\right)$
  
  
  
  (9RDP)  $\mathrm{Tau}=\left(t2t0.5\right)/\mathrm{1n}\left(\left(\mathrm{PDP}C1\right)/\left(\mathrm{PDP}C16\right)\right)$
  
  Where PDP is for pulmonary diastolic pressure and RDP is right ventricular diastolic time constant in pulmonary regurgitation patients.

• In tricuspid regurgitation patients
  Formulas for the calculation of right ventricular systolic time constant in tricuspid regurgitation patients are developed with a similar mathematical method, except:
  Three points, (t0.5, 0.5m/s), (t1, 1m/s) and (t2, 2m/s), are chosen on the ascending limb of the tricuspid regurgitation continuous-wave Doppler velocity curve Fig. (3). The final formulas are:
  
  
  (9RST1)  $\mathrm{Tau}=\left(t2t1\right)/\mathrm{1n}\left(\left(4+\mathrm{RAP}C\right)/\left(16+\mathrm{RAP}C\right)\right)$
  
  
  
  (9RST2)  $\mathrm{Tau}=\left(t2t0.5\right)/\mathrm{1n}\left(\left(1+\mathrm{RAP}C\right)/\left(16+\mathrm{RAP}C\right)\right)$
  
  where RST is for right ventricular systolic time constant in tricuspid regurgitation patients.
• In pulmonary regurgitation patients
  Formulas for the calculation of right ventricular systolic time constant in pulmonary regurgitation patients are developed with a similar mathematical method, except:
  Three points, (t0.5, 0.5m/s), (t1, 1m/s) and (t2, 2m/s), are chosen on the descending limb of the pulmonary regurgitation continuous-wave Doppler velocity curve Fig. (4). The final formulas are:
  
  
  (9RSP1)  $\mathrm{Tau}=\left(t1t2\right)/\mathrm{1n}\left(\left(\mathrm{PDP}C16\right)/\left(\mathrm{PDP}C4\right)\right)$
  
  
  
  (9RSP2)  $\mathrm{Tau}=\left(t0.5t2\right)/\mathrm{1n}\left(\left(\mathrm{PDP}C16\right)/\left(\mathrm{PDP}C1\right)\right)$
  
  where RSP is for right ventricular systolic time constant in pulmonary regurgitation patients.